Công Thức Lượng Giác: Khám Phá Thế Giới Hình Học
Chào bạn! Hôm nay, chúng ta sẽ cùng nhau khám phá một lĩnh vực thú vị trong toán học: lượng giác. Có thể bạn đã nghe qua về nó, nhưng liệu bạn có biết rằng lượng giác không chỉ là những công thức khô khan? Thực ra, nó là một phần quan trọng trong nhiều lĩnh vực khác nhau, từ vật lý đến kỹ thuật, và thậm chí cả trong âm nhạc! Hãy tưởng tượng, nếu không có công thức lượng giác, chúng ta sẽ khó có thể tính toán được những vấn đề liên quan đến độ cao của toà nhà, khoảng cách giữa các vì sao, hay thậm chí là hiểu được cách sóng âm truyền qua không gian. Bên cạnh đó, bảng công thức lượng giác cũng giống như một bản đồ giúp bạn dễ dàng tra cứu khi cần giải các bài toán phức tạp.
Lượng giác, đơn giản mà nói, là nghiên cứu về các mối quan hệ giữa các cạnh và góc của tam giác. Các công thức lượng giác giúp chúng ta tính toán những giá trị này một cách dễ dàng hơn. Bạn có thể hình dung nó như một chiếc bản đồ, hướng dẫn bạn đi qua những con đường phức tạp của toán học. Giải toán mời bạn cùng tham khảo bài viết dưới đây.

1. Các công thức lượng giác
Các công thức lượng giác cung cấp những công cụ mạnh mẽ để giải quyết nhiều bài toán từ hình học đến kỹ thuật, bao gồm công thức cộng, nhân đôi, hạ bậc, và biến đổi tích thành tổng. Hiểu và áp dụng chính xác các công thức này là chìa khóa để nắm vững lượng giác.
Công thức cơ bản

Công thức liên quan cến các cung đặc biệt

Công thức cộng

Công thức nhân đôi

Công thức nhân ba

Công thức hạ bậc
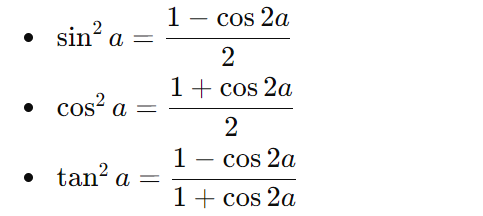
Công thức biến đổi tích thành tổng

Công thức biến đổi tổng thành tích

Công thức nghiệm của phương trình lượng giác cơ bản

2. Giải phương trình lượng giác
Giải phương trình lượng giác giúp tìm nghiệm của các phương trình có chứa các hàm lượng giác như sin, cos, tan, và cot. Quá trình giải thường liên quan đến việc sử dụng các công thức lượng giác, hằng đẳng thức, và biến đổi phương trình để tìm nghiệm thỏa mãn trong khoảng xác định trước.
Phương trình lượng giác cơ bản
Phương trình lượng giác cơ bản như một người bạn cũ, gặp là nhớ, chỉ cần một vài công thức là có thể giải quyết được. Ví dụ, các phương trình quen thuộc như sin x = 0 hay cos x = 1 đều có các công thức nghiệm rõ ràng mà bạn có thể thuộc lòng, chẳng hạn như:

Những phương trình này như những viên gạch nền, giúp bạn xây dựng kiến thức giải các phương trình phức tạp hơn.
Phương trình lượng giác chứa tham số
Phương trình lượng giác chứa tham số bạn phải rất cẩn thận trong từng bước để đảm bảo rằng mình không bỏ sót chi tiết. Với những phương trình như sin( x + a ) = b, bạn sẽ cần đến các công thức cộng hoặc biến đổi để đơn giản hóa chúng. Đôi khi, việc thử nghiệm các giá trị của tham số cũng là cách để tìm ra lời giải nhanh chóng và chính xác.
Phương trình lượng giác nghiệm nguyên
Giải phương trình nghiệm nguyên nghe có vẻ phức tạp, nếu bạn nắm rõ các công thức cơ bản và cách biến đổi, việc tìm nghiệm nguyên sẽ trở nên dễ dàng hơn rất nhiều. Đơn giản là kiểm tra xem với những giá trị cụ thể của x, phương trình của bạn có thoả mãn không. Bạn có thể bắt đầu từ những giá trị cơ bản như k = 0 , k = 1 sau đó thử nghiệm và đối chiếu kết quả.
Phương trình lượng giác nghiệm thuộc khoảng cho trước
Nếu bạn đã từng chơi trò tìm kho báu với bản đồ, bạn sẽ hiểu cảm giác giới hạn mình trong một khoảng cố định để tìm ra lời giải cho phương trình lượng giác nghiệm trong khoảng. Phương pháp ở đây là bạn tìm tất cả các nghiệm tổng quát trước, rồi sau đó chọn ra các nghiệm phù hợp trong khoảng yêu cầu. Ví dụ, nếu phương trình sin x = 1/2 có nghiệm tổng quát x = π /6 + 2 kπ và x = 5 π /6 + 2 kπ, bạn sẽ chỉ cần tìm nghiệm nào thuộc khoảng [ 0 , 2 π ].
3. Ứng dụng của công thức lượng giác
Công thức lượng giác không chỉ nằm trên sách vở hay trong các bài tập nhàm chán. Thực tế, chúng có nhiều ứng dụng thú vị mà có thể bạn không ngờ tới!
Trong toán học
Công thức lượng giác là chìa khóa để mở cánh cửa giải quyết các bài toán đạo hàm, tích phân hay tính toán diện tích tam giác. Chẳng hạn, trong đạo hàm, việc sử dụng các công thức lượng giác giúp đơn giản hoá việc tính đạo hàm của các hàm phức tạp. Hơn nữa, chúng rất quan trọng trong việc giải các tam giác, bất kể bạn đang tìm góc hay độ dài cạnh. Nó giống như việc ghép một bức tranh ,mỗi mảnh đều có vị trí của nó!
Trong vật lý
Bạn có biết rằng lượng giác còn giúp chúng ta hiểu rõ hơn về thế giới vật lý? Trong động học, việc tính toán vận tốc, gia tốc hay lực đều cần đến lượng giác. Trong điện từ học, các sóng điện từ được mô tả bằng các hàm sin và cos, và lượng giác giúp mô phỏng chúng một cách chính xác. Nói cách khác, lượng giác không chỉ là lý thuyết mà còn giúp chúng ta hiểu và mô phỏng các hiện tượng vật lý quanh ta.
Trong công nghệ thông tin
Bạn có từng thắc mắc tại sao đồ họa 3D trong game lại đẹp mắt đến thế? Đó là nhờ công thức lượng giác! Trong xử lý đồ họa, các vector và phép biến đổi hình ảnh đều cần lượng giác để tính toán góc quay, ánh sáng và màu sắc. Ngoài ra, trong xử lý tín hiệu, như âm thanh hoặc hình ảnh số, lượng giác giúp giải mã và biến đổi dữ liệu, mang lại những trải nghiệm số mượt mà.
4. Bài tập và ví dụ
Sau khi đã nắm vững lý thuyết, chúng ta cần thực hành ngay thôi!
Bài tập 1: Sử dụng công thức cộng
Đề bài:
Chứng minh rằng:
sin(45∘ + 30∘) = sin(45∘)cos(30∘) + cos(45∘)sin(30∘)
Hướng dẫn giải:
- Sử dụng công thức cộng của hàm :
sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
- Thay giá trị các góc và tính toán.
Bài tập 2: Sử dụng công thức nhân đôi
Đề bài:

Hướng dẫn giải:
- Sử dụng công thức nhân đôi:

Tính cos(x) từ sin(x) bằng định lý Pythagore.
Bài tập 3: Sử dụng công thức hạ bậc
Đề bài:
Tính giá trị của tích phân:

Hướng dẫn giải:
- Sử dụng công thức hạ bậc:

- Đưa về tích phân đơn giản và tính toán.
Nếu bạn cần hỗ trợ giải chi tiết hoặc thêm bài tập, mình rất sẵn lòng giúp!
5. Kết luận
Trong thực tế, việc ứng dụng công thức lượng giác rất phong phú. Bạn có thể tính toán quãng đường một chiếc tàu đi trên biển, dựa vào góc quay của nó. Hoặc nếu bạn đang làm kiến trúc sư, việc tính toán góc độ của ánh sáng chiếu vào một tòa nhà cũng sẽ cần đến lượng giác. Qua những bài tập và ứng dụng này, Giải Toán đã cho các bạn thấy lượng giác không còn là khái niệm trừu tượng nữa. Nó là công cụ mạnh mẽ giúp bạn hiểu rõ hơn về thế giới xung quanh và giải quyết các vấn đề thực tế.

